Topological Sorting and Kahn's Implementation

What is topological sorting?

This question has been haunting me for a while now. I did study SCCs once about 9 months back and I barely remember anything, so I decided to come back to the topic and try solving problems on this topic. But I know that a topological sorting is a prerequisite, and I’ve found the topic vague in terms of what it is, so I want to start off with clearly defining what it is.

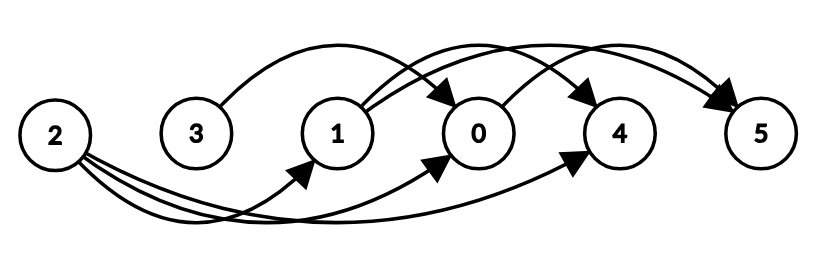
Given a DAG, the topologically sorted version represents the sequence of indices of nodes so that if there is a way from node $u$ to node $v$, then $u$ appears before $v$ in the sequence. And this holds for all pairs of nodes. Below is an example from csacademy.

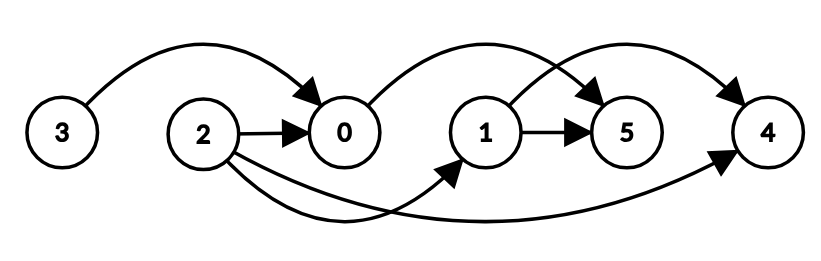
One thing to note is that there may be multiple topological sortings.

However there is always at least one in a DAG. This can be proved by induction since there will always be a node with in-degree 0 in a DAG. We place that at the front then remove it, and topologically apply. So there will always be at least one topological sorting given a DAG. Kahn’s algorithm functions based on this method.

In a non-DAG graph, there’s a contradiction of a sorted sequence when a cycle exists. Thus it only exists with DAGs.

Kahn’s Algorithm (BFS version)

We will apply the method explained earlier to now find the topologically sorted sequence. A good pseudocode algorithm is given on the wikipedia. Basically, we do a BFS starting from all nodes with indegree == 0, and we slowly progress by deleting nodes and adding the next nodes if their indegree == 0. Personally, I implemented as following:

//[O(V+E)] Given an adjacency list, returns the topologically sorted sequence.
//Returns empty vector when a cycle is detected.
vector<int> topological_sort(vector<vector<int>>& adj){
    vector<int> indegree(adj.size());
    for(auto &vec : adj) for(auto &v : vec) indegree[v]++;
    
    int n = adj.size();
    queue<int> q;
    vector<int> ret;
    for(int i=0;i<n;i++) if(indegree[i]==0) q.push(i);

    while(!q.empty()){
        int u = q.front(); q.pop();
        ret.push_back(u);

        for(int v : adj[u]) if(--indegree[v]==0) q.push(v);
    }

    for(int i=0;i<n;i++) if(indegree[i]>0) ret.clear();
    return ret;
}

Given an adjacency list, we set an indegree array to keep track of indegree, we then simulate removing edges by simply decrementing indegree. Since this way, indegree can reach negative values, we have to strictly check when indegree is 0, and in our final cycle check we must check if edges exist by checking if there are any positive indegrees. If so, we return an empty vector.

The cycle check process makes sense because the fact that there are leftover edges can exist only when there is a cycle since there are none with indegree 0 in this case. In this case, the bfs terminates once iteration is done, but the cycles aren’t included in the topological sort so the sequence breaks down and misses certain indices. So, for safety, we return an empty vector where later we can check in our main() code for cycles by just stating topological_sort().empty() == true.