Point in/on Convex Hull

Polygon Sectoring

A prerequisite is knowing that we clearly have a polygon, since if not the problem doesn’t even hold. We also have to have a clear polygon constructed. Refer to this page for more information on that topic.

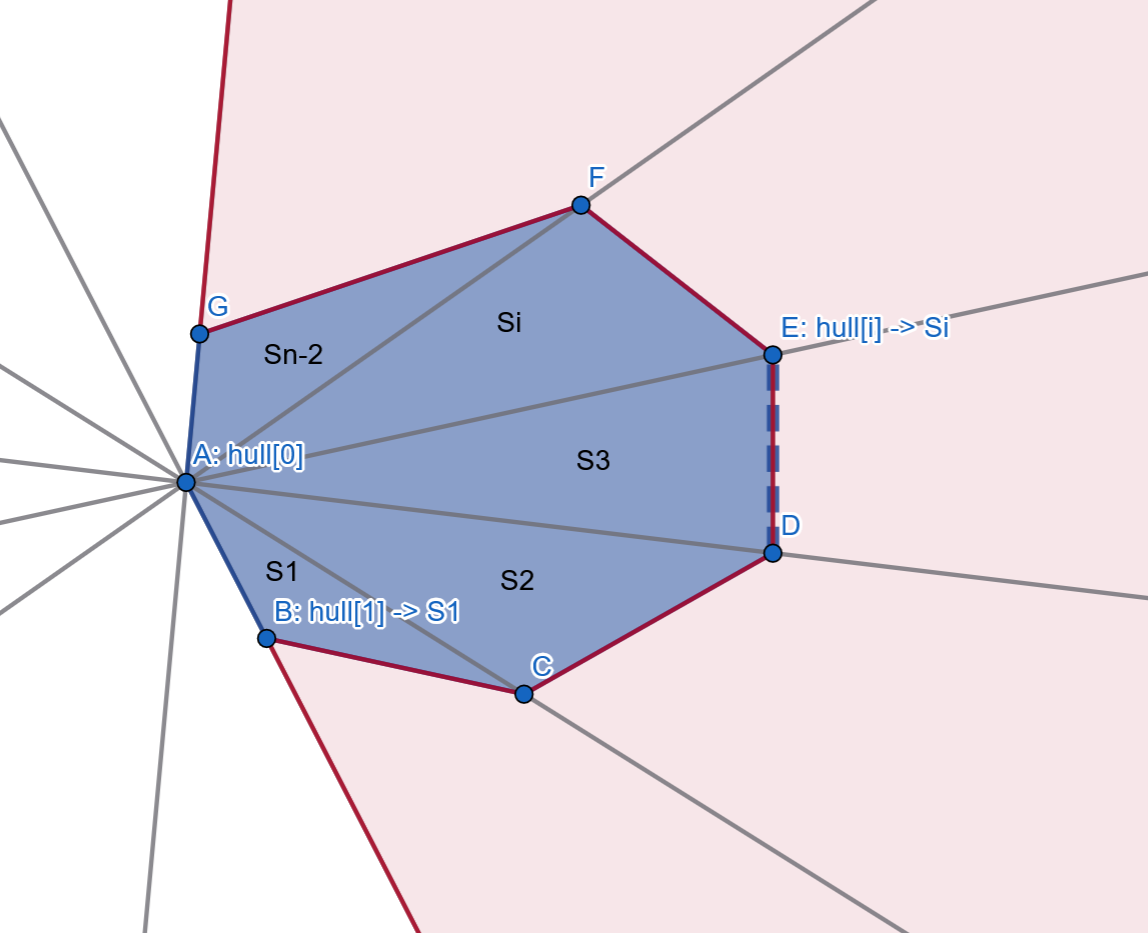
Also note that following our method of construction, we already have a good order so that the leftmost bottommost point is set as $\text{hull}[0]$. Setting this as a sort of “axis”, we can now iterate through our hull knowing we can sector as following:

Basically, we can divide the polygon into $n-2$ sectors. Note that this works for the most minimum case, where $n=3$ as well. So, we can simplify the point in polygon check into a few steps:

1. Check if the point belongs in any candidate sectors. We define a “candidate sector” as the infinitely extended sector from our original sector, the whole sector including both the blue and red colored areas.
2. Check if it is inside the sector given the candidate sector it is in, which just means check if is in the blue colored area.

Point in Polygon

Now about the aforementioned steps in detail.

We can do the first check by iterating over each point indexed 1~n-1. We want to find the last position where $\text{above}(i)$ is -1, where we define the above function as the CCW state of the point relative to the line segment connecting vertices 0 → i aka the segment that crosses point i from our pivot.

We could do this iteratively, but the main reason of doing this is to do this in logarithmic time. We can reduce iterations to $O(\log n)$ since there is monotonicity in our above function. We can find the upper bound of 1 among above, with a greater comparator since our monotonicity is that it’s decreasing. This will return the first time it is NOT 1, so we want to refer to that index - 1. But here we can clear off some edge cases before continuing. The first is when the upper bound equals the begin iterator. That means that all are not 1, and thus the point does not lie on any candidates. The second is when the upper bound equals the end iterator. That means all are 1, and also that it lies above our very end line that doesn’t really point to a specific sector, thus the point does not lie on any candidates. We can instantly return false in both cases.

Now we know it belongs to some candidate sector, and specifically which candidate sector being the upper bound - 1. Let $i = \text{upper bound} - 1$. The point is in candidate sector $S_i$. All we have to check is if the point is at the relative left of the line segment connecting $i \to i+1$, which we can do with CCW. We check if this is 1, where we return true. Else return false.

But there is one edge case, where the point is on $0\to n-1$. This shouldn’t pass the test since it’s on the border, but it does following our logic. We will add a separate check for this before any of the other checks take place. We can do this by checking if the CCW of the point and mentioned segment is 0, and CCW of the point and the segment right before that is strictly NOT 1, and CCW of the point and the first segment is NOT -1.

We can also just use dot product which is honestly the easiest. Simply checking if the dot product of the vector of the segment and the vector from one endpoint to the point is positive from both sides works best.

Note that this checks if it is strictly inside. Modifications to check if the point is on the polygon is mentioned below. Also, the reason we use partition_point is because we have a specific condition. We can’t construct an entire array and find the exact upper bound with the usual method since that way it will cost O(n).

bool point_in_polygon(vector<pll>& polygon, pll point){
    if(point_on_segment(polygon.back(), polygon.front(), point)) return false;

    auto ub = partition_point(polygon.begin()+1, polygon.end(), [&](const pll& polygonPoint){
        return CCW(polygon.front(), polygonPoint, point)==1;
    });
    if(ub == polygon.begin()+1 || ub == polygon.end()) return false;
    int idx = ub - polygon.begin();
    return CCW(polygon[idx-1], polygon[idx], point) == 1;
}

Point on Polygon

The most obvious step is to change the CCW check in the transition from a candidate sector to a sector to strictly 1 to not -1. This means 0, meaning being on the segment, is now allowed. However we need to account for two specific edge cases. Remember how we checked for non 1s through the binary search? We need to be generous on the edge connecting $0\to 1$. Before any of the aforementioned processes, we first check if it the given point is on this edge. After that, we can continue with our modified check with CCW = 0 being allowed. We can do this with the method we used for the edge case in point in polygon check.

In short, all we have to do is switch the first condition and return value, along with the final return condition

bool point_on_polygon(vector<pll>& polygon, pll point){
    if(point_on_segment(polygon[0], polygon[1], point)) return true;

    auto ub = partition_point(polygon.begin()+1, polygon.end(), [&](const pll& polygonPoint){
        return CCW(polygon.front(), polygonPoint, point)==1;
    });
    if(ub == polygon.begin()+1 || ub == polygon.end()) return false;
    int idx = ub - polygon.begin();
    return CCW(polygon[idx-1], polygon[idx], point) != -1;
}